Prinzip des Archimedes
Das archimedische Prinzip beschreibt den Verlust an Gewichtskraft, d. h. den Auftrieb, den ein Körper beim Eintauchen in eine Flüssigkeit (präziser in ein Fluid) erfährt.
Es erklärt im Tauchsport den physikalischen Hintergrund hinter der Tarierung.
Inhaltsverzeichnis
Grundwissen für Open Water Diver* (OWD*)
Taucht man einen Körper ins Wasser, so wirkt eine Kraft nach unten – die Abtriebskraft – auf ihn, die ihn sinken lässt. Diese Kraft wird durch die Masse des Körpers bestimmt.
Weiterhin wirkt eine Kraft nach oben – die Auftriebskraft – auf ihn, die ihn aufsteigen lässt. Das Prinzip des Archimedes besagt, dass ein Körper im Wasser soviel an Gewichtskraft verliert, d. h. soviel an Auftriebskraft erhält, wie das von ihm verdrängte Wasser wiegt. Die Auftriebskraft, die auf einen Körper wirkt, wird also durch sein Volumen (und die Dichte des Wassers) bestimmt.
Je nachdem, wie sich die beiden Kräfte zueinander verhalten, sinkt der Körper ab, steigt auf oder schwebt:
- Ist die Abtriebskraft größer als die Auftriebskraft, dann sinkt der Körper ab. Er hat effektiv Abtrieb.
- Ist die Auftriebskraft größer als die Abtriebskraft, dann steigt der Körper auf. Er hat effektiv Auftrieb.
- Wenn beide Kräfte gleich groß sind, schwebt der Körper. Er ist im hydrostatischen Gleichgewicht bzw. ist austariert.
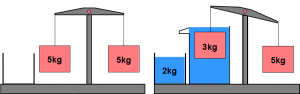
An der Abbildung ganz oben kannst du dir das archimedische Prinzip veranschaulichen: Taucht man einen Körper mit einem Gewicht von 5 kg und einem Volumen von 2 l in Süßwasser, so verdrängt er 2 kg Wasser. Das Gewicht des verdrängten Wassers wirkt auf ihn als Auftriebskraft und somit wiegt er scheinbar nur noch 3 kg.
Der Salzgehalt des Wassers hat zudem einen Einfluss auf die Auftriebskraft. Salzwasser besitzt eine höhere Dichte als Süßwasser. Das bedeutet, dass das Salzwasser bei gleichem Volumen schwerer ist als Süßwasser. Ein Körper erfährt also im Salzwasser eine höhere Auftriebskraft als im Süßwasser.
Wissen für fortgeschrittene Taucher (ED**)
Unterschied zwischen Süß- und Salzwasser
Die Auftriebskraft wird neben dem Volumen des verdrängten Wassers auch durch dessen Dichte bestimmt (siehe Abschnitt Physikalische Herleitung). Süßwasser hat eine Dichte von 1,0 kg/dm3 wohingegen die Dichte von Salzwaser im Schnitt 1,035 kg/dm3 beträgt. Taucht man den Körper aus obigem Beispiel in Salzwasser, so beträgt das verdrängte Volumen immer noch 2 l, allerdings beträgt das Gewicht des verdrängten Wassers 2,07 kg. Ein Körper erfährt im Salzwasser somit etwa 3,5% mehr Auftrieb als im Süßwasser, da das verdrängte Volumen an Salzwasser 3,5% schwerer ist.
Für die Bestimmung der Bleimenge bedeutet das, dass du bei gleicher Ausrüstungskonfiguration im Salzwasser mehr Blei mitnehmen musst. Besitzt der Taucher incl. Tauchausrüstung beispielsweise ein Volumen von 100 Liter, so sind im Salzwasser 3,5 kg mehr Blei als im Süßwasser notwendig.
Expertenwissen (DM***)
Physikalische Herleitung
Auftriebskraft
Die Ursache, weshalb ein Körper in einer Flüssigkeit eine Auftriebskraft erfährt, ist der Druckunterschied zwischen der Ober- und Unterseite des Körpers.
Auf eine Oberfläche mit dem Flächeninhalt [math]A[/math] wirkt bei einem Druck [math]p[/math] eine Kraft [math]F[/math]:
- [math]F = p \cdot A[/math]
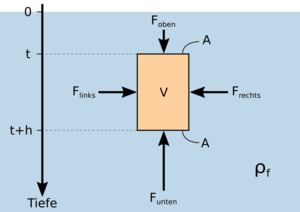
Taucht man einen Körper in eine Flüssigkeit, so wirken allseitig Kräfte auf ihn. Die horizontal wirkenden Kräfte (d. h. die von links und rechts wirkenden) kompensieren sich genau, da der Umgebungsdruck auf beiden Seiten unabhängig von der Form des Körpers identisch ist. Ober- und Unterseite des Körpers befinden sich jedoch in unterschiedlichen Tiefen und sind somit einem unterschiedlichen Umgebungsdruck ausgesetzt. Die auf die Unterseite wirkende Kraft ist wegen des höheren Umgebungsdrucks größer als die auf die Oberseite wirkende, was in Summe zu einer nach oben wirkenden Kraft auf den Körper führt und dem Körper Auftrieb verleiht.
Man geht ohne Beschränkung der Allgemeinheit davon aus, dass der Körper regelmäßig geformt ist, d. h. Ober- und Unterseite den gleichen Flächeninhalt [math]A[/math] aufweisen und seine Höhe [math]h[/math] beträgt. Die Auftriebkraft [math]F_{\text{auf}}[/math] berechnet sich somit zu:
- [math]F_{\text{auf}} = F_{\text{unten}} - F_{\text{oben}} = (p_{\text{unten}} \cdot A) - (p_{\text{oben}} \cdot A) = (p_{\text{unten}} - p_{\text{oben}}) \cdot A[/math]
Der Umgebungsdruck auf der Oberseite ergibt sich aus dem Atmosphärendruck [math]p_{\text{atm}}[/math] und der Gewichtskraft der auf der Oberseite in der Tiefe [math]t[/math] lastenden Wassersäule (Volumen [math]A \cdot t[/math]):
- [math]p_{\text{oben}} = \frac{g \cdot \rho_{\text{f}} \cdot A \cdot t}{A} + p_{\text{atm}}[/math]
Die Konstante [math]g[/math] wird als Fallbeschleunigung bezeichnet, [math]\rho_{\text{f}}[/math] ist die Dichte der Flüssigkeit.
Analog zu der Oberseite beträgt der Druck an der Unterseite [math]p_{\text{unten}}[/math] somit:
- [math]p_{\text{unten}} = \frac{g \cdot \rho_{\text{f}} \cdot A \cdot (t + h)}{A} + p_{\text{atm}}[/math]
Die Auftriebskraft berechnet sich damit zu:
- [math]F_{\text{auf}} = g \cdot \rho_{\text{f}} \cdot A \cdot h = g \cdot \rho_{\text{f}} \cdot V[/math]
Da [math]A \cdot h[/math] dem Volumen [math]V[/math] des Körpers und damit dem Volumen der verdrängten Flüssigkeit entspricht, hängt die Auftriebskraft nur von diesem und der Dichte der Flüssigkeit ab. Der Körper erfährt also eine Auftriebskraft, die der Gewichtskraft der von ihm verdrängten Flüssigkeitsmenge entspricht. Dieser Zusammenhang gilt unabhängig von Lage und Form des Körpers:
- Dreht man den dargestellten Körper beispielsweise um 90°, ist die Oberfläche [math]A[/math] der Ober- und Unterseite größer. Allerdings wirkt auf die Unterseite eine geringere Kraft, da sie sich in geringerer Tiefe befindet.
- Verwendet man beispielsweise einen kegelförmigen Körper, so ist die Oberfläche der Ober- und Unterseite unterschiedlich groß ist. Auf die nun schiefen Seitenflächen wirken dann aber Kräfte nach oben bzw. unten.
Abtriebskraft
Die Abtriebskraft [math]F_{\text{ab}}[/math], die auf den Körper wirkt, ist seine Gewichtskraft. Mit der Dichte [math]\rho_{\text{k}}[/math] des Körpers, berechnet sie sich zu:
- [math]F_{\text{ab}} = g \cdot m = g \cdot \rho_{\text{k}} \cdot V[/math]
Resultierende Kraft
Zieht man die Abtriebskraft [math]F_{\text{ab}}[/math] von der Auftriebskraft [math]F_{\text{auf}}[/math] ab, so ergibt sich die resultierende Kraft [math]F[/math] auf den Körper. Ist diese positiv, dann hat der Körper Auftrieb, ist sie hingegen negativ, hat er Abtrieb.
- [math]F = F_{\text{auf}} - F_{\text{ab}} = g \cdot \rho_{\text{f}} \cdot V - g \cdot \rho_{\text{k}} \cdot V = g \cdot (\rho_{\text{f}} - \rho_{\text{k}}) \cdot V[/math]
Somit bestimmt der Dichteunterschied zwischen Körper und Flüssigkeit, ob der Körper Auftrieb hat, Abtrieb hat oder sich im hydrostatischen Gleichgewicht befindet: Hat der Körper eine höhere Dichte als die Flüssigkeit, hat er Abtrieb. Ist seine Dichte geringer, hat er Auftrieb. Bei identischen Dichten ist er austariert.
Bei der Tarierung ändern sich das Volumen [math]V[/math] des Tauchers und seine effektive Dichte [math]\rho_{\text{k}}[/math] gegenläufig. Da die Änderung der Masse durch die geänderte Gasmenge, also das Produkt aus beiden, vernachlässigbar ist, ändert sich die Abtriebkraft nicht. Die Auftriebskraft hingegen verändert sich, da sie vom Volumen des Tauchers bestimmt wird.
Berechnungsbeispiel
Nachfolgend soll der Auf- bzw. Abtrieb von Taucherflaschen aus verschiedenen Materialien und bei unterschiedlichen Füllständen berechnet werden. Verglichen werden im Süßwasser Stahl- und Aluminiumflaschen mit 10 l Inhalt jeweils auf 200 bar gefüllt und mit einem Restdruck von 50 bar. Die Berechnungen sind in untenstehender Tabelle zusammengefasst.
Die Masse des Flaschenmaterials selbst beträgt 11,2 kg bei der Stahlflasche und 12,4 kg bei der Aluminiumflasche (jeweils ohne Flaschenventil).
Zur Berechnung der Auftriebskraft muss das Gesamtvolumen bekannt sein. Dieses setzt sich aus dem Flascheninhalt und dem Volumen des Flaschenmaterials zusammen. Letzteres kann aus der Masse des Flaschenmaterials und dessen Dichte berechnet werden.
Die Abtriebskraft wird bestimmt durch die Masse des Flaschenmaterials und die Masse der enthaltenen Luft. Für die Dichte der Luft wird angenommen, dass sie 1,3 g/dm3 bei einem Bar beträgt und mit dem Fülldruck [math]p_{\text{in}}[/math] linear zunimmt. Das bedeutet, dass die Masse von Luft 1,3 Gramm pro Barliter beträgt.
| Größe | Gleichung | Stahlflasche | Aluminiumflasche | ||
|---|---|---|---|---|---|
| Flascheninhalt | [math]V_{\text{in}}[/math] | 10 l | 10 l | ||
| Masse Flaschenmaterial | [math]m_{\text{fm}}[/math] | 11,2 kg | 12,4 kg | ||
| Dichte Flaschenmaterial | [math]\rho_{\text{fm}}[/math] | 7,9 kg/dm3 | 2,71 kg/dm3 | ||
| Volumen Flaschenmaterial | [math]V_{\text{fm}} = \frac{m_{\text{fm}}}{\rho_{\text{fm}}}[/math] | 1,4 l | 4,6 l | ||
| Gesamtvolumen | [math]V = V_{\text{in}} + V_{\text{fm}}[/math] | 11,4 l | 14,6 l | ||
| Auftriebskraft | [math]F_{\text{auf}} = g \cdot \rho_{\text{f}} \cdot V[/math] | 112 N | 143 N | ||
| Fülldruck | [math]p_{\text{in}}[/math] | 200 bar | 50 bar | 200 bar | 50 bar |
| Masse Luft | [math]m_{\text{in}} = \frac{1,3\ \text{g}}{\text{bar l}} \cdot V_{\text{in}} \cdot p_{\text{in}}[/math] | 2,60 kg | 0,65 kg | 2,60 kg | 0,65 kg |
| Abtriebskraft | [math]F_{\text{ab}} = g \cdot (m_{\text{fm}} + m_{\text{in}})[/math] | 135 N | 116 N | 147 N | 128 N |
| Auftrieb (+) / Abtrieb (-) | [math]F = F_{\text{auf}} - F_{\text{ab}}[/math] | - 23 N | - 4 N | - 4 N | + 15 N |
| [math]\frac{F}{g}[/math] | - 2,3 kg | - 0,4 kg | - 0,4 kg | + 1,5 kg | |
Die Stahlflasche hat im voll gefüllten Zustand einen deutlichen Abtrieb und ist bei 50 bar Restdruck fast neutral. Obwohl die Aluminiumflasche eine größere Masse als die Stahlflasche hat, ist sie im voll gefüllten Zustand fast neutral und hat bei 50 bar Restdruck deutlich Auftrieb. Die Ursache ist die geringere Dichte von Aluminium: Bei ähnlicher Masse ist das Volumen des Materials der Aluminiumflasche deutlich größer und erzeugt somit deutlich mehr Auftrieb.
Beide Flaschen verlieren während eines Tauchgangs soviel an Abtrieb, wie die verbrauchte Luftmenge wiegt. Dies muss bei der Bestimmung der Bleimenge berücksichtigt und entsprechend vorgehalten werden.